Argument Form

A crucial step in understanding and evaluating an argument is to identify its form. Consider the following argument:

Argument 1: Ann will either get an A or B in PHIL 171. Ann will not get a B in PHIL 171. So, Ann will get an A in PHIL 171.

This argument consists of three statements:

1. Ann will either get an A or B in PHIL 171.
2. Ann will not get a B in PHIL 171.
3. Ann will get an A in PHIL 171.

Statements 1 and 2 are the premises and statement 3 is the conclusion. Using our notation "$\Rightarrow$" for identifying the conclusion, argument 1 can be represented as follows:

Ann will either get an A or B in PHIL 171, Ann will not get a B in PHIL 171 $\Rightarrow$ Ann will get an A in PHIL 171

We can visualize this argument as follows:

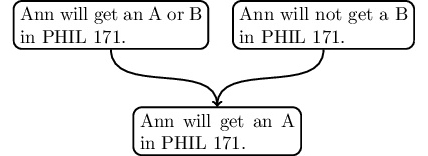
An arrow from one statement to another statement means that the first statement is intended to support or provide evidence for the second statement. However, the above diagram misses something very important about the structure of argument 1. The conclusion of argument 1 is not supported by each individual premise, but rather it is supported by combining the two premises. We can highlight this aspect of the argument by adding a line that links the two premises:

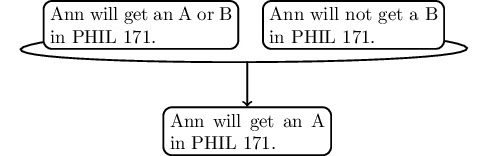
While the above representation of argument 1 is better since it explicity identifies the premises that are connected, there are still problems. In particular, it is not clear in the above diagram why the two premises are connected. Looking more closely at the premises reveals additional structure that helps evaluate the argument.

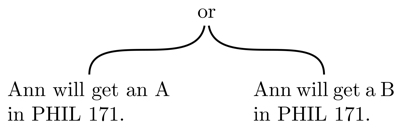
The first premises can be decomposed as two statements connected by the word "or": That is, the "Ann will get an A or B in PHIL 171" can be paraphrased as:

Ann will get an A in PHIL 171 or Ann will get a B in PHIL 171.

The following diagram represents the structure of the above statement.

Similarly, the second premise can be decomposed as applying the word "not" to a statement: That is, "Ann will not get a B in PHIL 171" can be paraphrased as:

It is not the case that Ann will get a B in PHIL 171.

The form of argument 1 can be described as folows. Argument 1 involves two basic statements "Ann will get an A in PHIL 171" and "Ann will get a B in PHIL 171". The first premise is an "or"-statement connecting the two basic statements, the second premise is a "not"-statement negating the second basic statement, and the conclusion is the first basic statement. The following diagram with the two basic statements highlighted in blue and red is a better representation of argument 1.

Replacing the blue and red box with different statements leads to arguments that have the same form as argument 1. For instance, the following argument has the same form as argument 1:

Lily is going to paint or sketch. Lily is not going to sketch. So, Lily is going to paint.

For much of this course, we are interested in the form of arguments rather than any specific argument. We can depict the form of argument 1 by adding empty slots for the two basic statements in the above diagram. The blue empty slots are labeled with $X$ and the red empty slots are labeled with $Y$:

Using the labels for the empty slots and the key words "or" and "not", a simpler way to represent the form of argument 1 is:

$$X\text{ or } Y, \text{not } Y\Rightarrow X$$

Variables and Abstract Arguments

In the remainder of this text we will use $X$, $Y$ and $Z$ (possibly with subscripts) as variables that range over statements. We call an argument with variables an abstract argument. When the variables in an abstract argument are replaced with statements, we say that the resulting argument is an instance of the abstract argument. For example, the following is an abstract argument:

$$X\text{ or } Y, \text{not } Y \Rightarrow X$$

And, the following is an instance of this abstract argument:

Ann had pizza or tacos. Ann did not have tacos. $\Rightarrow$ Ann had pizza.

Notes about variables and abstract arguments

1. Each variable represents a single statement.

2. Different variables can represent the same statement.

3. The words or and not are logical constants that describe the logical form of the statements in an abstract argument.

4. Variables can be substituted with complex sentences (e.g., sentences containing logical constants such as "or" and "not"). For instance, the following is an instance of the above abstract argument:

   Ann will get an A or a B in PHIL 171, or Ann will drop PHIL 171. Ann will not drop PHIL 171. So, Ann will get an A or a B in PHIL 171.

5. It is required that an instance of an abstract argument matches the form exactly. For instance, the following is not an instance of the above abstract argument:

   Ann will get an A or B in PHIL 171. Ann will not get an A in PHIL 171. So, Ann will get a B in PHIL 171.

6. It is important to remember that the symbol "$\Rightarrow$" is used to separate the premises from the conclusion in an argument. Writing "$X, Y \Rightarrow Z$" does not mean that this is a "good" pattern of reasoning.

The process of replacing variables with statements in an abstract argument should remind you of a similar process in algebra. In the algebraic equation

$$(x +y)^2=x^2+2xy+y^2$$

any way of replacing the variables "$x$" and "$y$" with numbers results in a true equality. For instance, if $x$ is $1$ and $y$ is $2$, then substituting results in the following true arithemtic statement:

$$(1+2)^2=1^2 + 2\times 1\times 2 + 2^2$$

(note that both sides of the equality evaluate to $9$). In algebra, variables are used to help identify general arithmetic facts. In this course, we use variables to identify interesting patterns of reasoning.

In this course, we will use a formal language to express the statements in an argument. This formal language will be introduced in the next chapter. There are positive and negative aspects to taking this more abstract approach to studying reasoning. One downside is that our formal language will not be able to represent everything that can be expressed in English. Furthermore, it is not always clear how to translate English sentences into our formal language. The upside is that a formal language removes ambiguity that makes it difficult to evaluate patterns of reasoning in English. To illustrate, consider the following argument:

Ann is in College Park. College Park is in Maryland. So, Ann is in Maryland.

This is an instance of the following reasoning pattern:

$x$ is in $y$. $y$ is in $z$. So, $x$ is in $z$.

This seems like a good reasoning pattern. But, it is possible to find items to substitute for the variables resulting in an argument in which the premises are all true but the conclusion is false (see problem 7 below).

Practice Questions

1. Consider the argument pattern $X\Rightarrow Y$. True or False: The argument:

   Lily had pizza. So, Lily drank a beer.

   is an instance of the above reasoning pattern.

   True

   False

   ​

   Both "Lily had pizza" and "Lily drank a beer" express propositions (i.e., they are declarative sentences), so they can be substituted for the variables $X$ and $Y$.

2. Consider the argument pattern $X\Rightarrow Y$. True or False: The argument:

   Lily had pizza. So, Lily had pizza.

   is an instance of the above reasoning pattern.

   True

   False

   ​

   This is true. When replacing variables with statements, you can replace different variables with the same statement. Note that it is also true in algebra that different variables can be replaced with the same number: E.g., $x+y=4$ is true when $x=y=2$.

3. Consider the argument $X, Y\Rightarrow Z$. What is the argument that results when you substitution $X$ with "Ann will get an A or B in PHIL 171", $Y$ with "Ann will not get an B in PHIL 171" and $Z$ with "Ann will get an A in PHIL 171".?

   Ann will not get an B in PHIL 171. Ann will get an A or B in PHIL 171. So, Ann will get an A in PHIL 171.

   Ann will get an A or B in PHIL 171. Ann will not get an B in PHIL 171. So, Ann will get an A in PHIL 171.

   Both of the above are correct substitutions.

   ​

   When you subtitute for variables in an abstract argument, it is important that you do not change anything except replacing the variables.

4. True or False: $X\Rightarrow (Y\Rightarrow Z)$ is an abstract argument.

   True

   False

   ​

   In this text, the symbol "$\Rightarrow$" is used to identify the conclusion of an argument. The conclusion must be a statement not another argument, so iterating the "$\Rightarrow$" symbol does not make sense. (Note that, later in the course, we will use a different symbol "$\rightarrow$" that can be iterated.)

5. How many different abstract arguments can you construct from two variables $X$ and $Y$?

   1

   2

   4

   6

   ​

   Each of the following are different abstract arguments:

   1. $X\Rightarrow Y$ ($X$ is the premise and $Y$ is the conclusion)
   2. $Y\Rightarrow X$ ($Y$ is the premise and $X$ is the conclusion)
   3. $X\Rightarrow X$ ($X$ is the premise and the conclusion)
   4. $Y\Rightarrow Y$ ($Y$ is the premise and the conclusion)
   5. $\Rightarrow X$ (there are no premises and $X$ is the conclusion)
   6. $\Rightarrow Y$ (there are no premises and $Y$ is the conclusion)

6. What is the abstract argument for which the following argument is an instance?

   Ann will get an A or B in PHIL 171. Ann will not get an A in PHIL 171. So, Ann will get a B in PHIL 171.

7. Find objects to subtitute for $x$, $y$ and $z$ in the following reasoning pattern that results in an argument in which the premises are true and the conclusion is false.

   $x$ is in $y$. $y$ is in $z$. So, $x$ is in $z$.

8. Consider the reasoning pattern: $X\text{ or }Y, \text{not } X \Rightarrow Y$. Which argument is an instance of this reasoning pattern?

   A1: My keys are either in my office or locked in my car. My keys are not in my office. My keys are locked in my car.

   A2: My keys are either in my office or locked in my car. My keys are not locked in my car. My keys are in my office.

   ​

   Let $X$ be "My keys are in my office" and $Y$ be "My keys are locked in my car". A2 is a different reasoning pattern: $Y\text{ or }X, \text{not X} \alpha\Rightarrow Y$.

9. Consider the reasoning pattern: $X\text{ or } Y, \text{not }X \Rightarrow Y$. Which argument is an instance of this reasoning pattern?

   A1: Ann will not get an A in PHIL 171. Ann will get an A or B in PHIL 171. So, Ann will get a B in PHIL 171.

   A2: Ann will get an A or B in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an B in PHIL 171.

   A3: Ann will get an A or B in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an A in PHIL 171.

   ​

   Let $X$ be "Ann will get an A in PHIL 171" and $Y$ be "Ann will get a B in PHIL 171". A1 is an instance of $\text{ not } X, X\text{ or } Y\Rightarrow Y$. A3 is an instance of $X\text{ or } Y, \text{ not } X \Rightarrow X$. The crucial point is that the order of the premises matters when stating an argument.

10. Consider the reasoning pattern: $X\text{ or } Y, \text{not }Y \Rightarrow X$. Which argument is an instance of this reasoning pattern?

    A1: Ann will get an A or B in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an B in PHIL 171.

    A2: Ann will get a B or A in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an B in PHIL 171.

    ​

    Let $X$ be "Ann will get an B in PHIL 171" and $Y$ be "Ann will get a A in PHIL 171". Of course, "Ann will get an A or B in PHIL 171" and "Ann will get a B or A in PHIL 171" mean the same thing, but this is a question about pattern matching, and A2 is the only one that matches the reasoning pattern. A1 is an instance of $Y\text{ or } X, \text{ not } Y \Rightarrow X$.

11. Consider the reasoning pattern: $X\text{ or } Y, \text{not }Y \Rightarrow X$. Which argument is an instance of this reasoning pattern?

    A1: Ann will get an A or B in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an B in PHIL 171.

    A2: Ann will get a B or Ann will get an A in PHIL 171. Ann will not get a B in PHIL 171. So, Ann will get an A in PHIL 171.

    A3: Ann will get a A or Ann will get an A in PHIL 171. Ann will not get a A in PHIL 171. So, Ann will get an A in PHIL 171.

    None of the above of instances of the abstract argument.

    ​

    Let $X$ and $Y$ both be "Ann will get an A in PHIL 171". Recall, that variables may represent the same statement.