Classifying Formulas
Classifying a single formula#
Consider a truth table for the formulas , , and :
These formulas can be placed in different categories:
- Always true: The formula is true in every row of the truth table.
- Always false: The formula is false in every row of the truth table.
- Sometimes true and sometimes false: The formula is true in the first three rows and false in the last row.
In fact, any formula can be placed into one of the above three categories. The following terminology will be used to classify formulas.
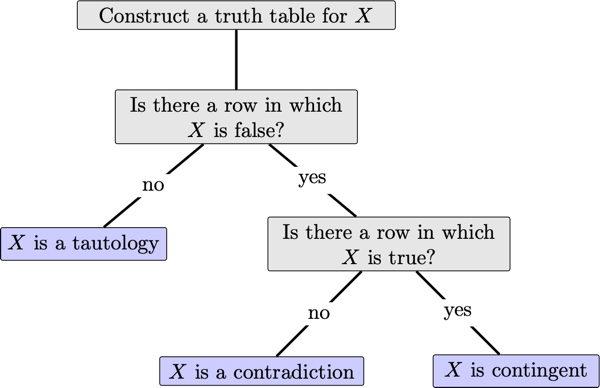
A formula is a tautology if every truth value assignment makes true.
A formula is a contradiction if every truth value assignment makes false.
A formula is a contingent formula if there is a truth value assignment that makes true and a truth value assignment that makes false.
The following is a summary of the procedure to use a truth table to classify a formula as either a tautology, contingent or a contradiction:
Classifying collections of formulas#
In addition to classifying formulas, we use truth tables to identify interesting relationships between formulas. To illustrate, consider a truth table for the formulas , , and :
This truth table reveals the following realtionships between the four formulas:
- In every row, and have different truth values.
- In every row, and have the same truth value.
- The formulas and are never true in the same row, but there are rows in which they are both false (rows 2 and 3).
- There is a row in which the formulas and are both true (row 4).
We introduce the following terminology to classify the relationship between formulas.
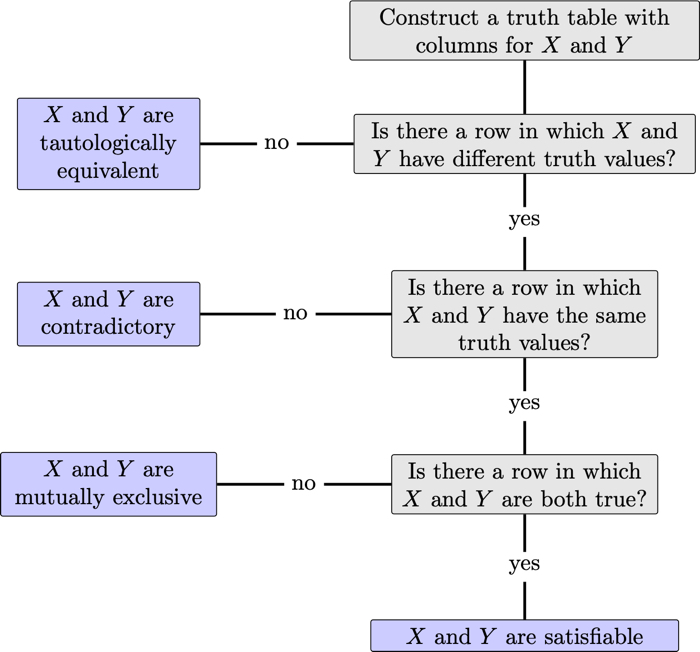
The formulas and are tautologically equivalent if every truth value assignment gives the same truth value to and .
The formulas and are contradictory if every truth value assignment gives the different truth values to and .
The formulas and are mutually exclusive, also called contraries, if there is no truth value assignment in which and are both true.
The formulas and are satisfiable if there is a truth value assignment in which both and are true.
The following is a summary of the procedure to use a truth table to classify two formulas and as either tautologically equivalent, contradictory, satisfiable or mutually exclusive:
There are two important observations about classifying two formulas:
If and are contradictory, then they are also mutually exclusive. But, if and are mutually exclusive, then they may not be contradictory (since there may be a truth value assignment that makes both false).
If and are tautologically equivalent, then they may or may not be satisfiable. For instance, if and are both contradictions, then they are tautologically equivalent, but they are not satisfiable.
Practice Questions#
I. Answer the following true/false questions.
- There is a formula that is both contingent and a tautology.
For any formula , if is contingent, then is also contingent.
For all formulas and , if is a tautology and is contingent, then is a tautology.
For all formulas and , if is a tautology and is contingent, then is a tautology.
For all formulas and , if is a contradiction and is contingent, then is a tautology.
For all formulas and , if is contingent and is contingent, then is contingent.
For all formulas and , if and are tautologically equivalent, then and are tautologically equivalent.
II. Classify the following formulas as contingent, a contradiction or a tautology.
III. Classify the following pairs of formulas as tautologically equivalent, contradictory, contraries, or satisfiable.
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and
- and