Formulas
This section introduces formulas of propositional logic. Each formula is an expression that represents a statement, or a proposition.
The first step is to settle on notation for the basic statements that are used to build up more complex statements.
Capital letters from the beginning and middle of the alphabet () are atomic proposition (also called a sentence letter). Sometimes we will use subscripts to denote atomic propositions, i.e., . This will ensure that we never run out of symbols to use for atomic propositions.
Capital letters from the end of the alphabet (, , and ), possibly with subscripts (e.g., , , ), are variables that range over any formula.
In addition to atomic propositions, formulas will be constructed using the symbols (the left and right parentheses and the Boolean connectives):
Formulas are constructed according to the following rules.
- Any atomic proposition , is a formula.
- If is a formula, then is a formula.
- If and are formulas, then so is , , and .
- Nothing else is a formula.
Examples of formulas constructed using these rules include:
- ,
- ,
- , and
- .
It is important to understand exactly how the above rules are used to construct these formulas:
is a formula:
- Since is an atomic proposition, is a formula according to rule 1.
- Since is a formula, is a formula according to rule 2.
- Since and are formulas, is a formula according to rule 3.
is a formula:
- Since and are atomic propositions, they are formulas according to rule 1.
- Since and are formulas, is a formula according to rule 3.
- Since is a formula, is a formula according to rule 2.
is a formula:
- Since , and are atomic propositions, they are formulas according to rule 1.
- Since is a formula, is a formula according to rule 2.
- Since and are formulas, is a formula according to rule 3.
- Since and are formulas, is a formula according to rule 3.
is a formula:
- Since and are atomic propositions, they are formulas according to rule 1.
- Since and are formulas, is a formula according to rule 3.
- Since is a formula, is a formula according to rule 2.
- Since is a formula, is a formula according to rule 2.
Examples of strings of symbols that are not formulas according to the above rules include:
- : Rule 3 requires that a single connective is written between two formulas.
- : Rule 3 requires that a connectives is written between two formulas.
- or : Rule 2 does not use parentheses when constructing a formula.
- : Rule 3 requires that parentheses are placed around the constructed formula. Note that we will introduce some conventions to simplify our notation. According to these conventions, will be a formula.
- : According to the official definition, only capital letters can be used as atomic propositions. Of course, there is no difficulty if we decide that lowercase letters can also be used as symbols to represent atomic propositions.
Variables vs. Atomic Propositions
In many situations, we treat variables and atomic propositions similarly. However, there is an important difference between formulas with variables and formulas with atomic propositions. For example, consider the following two formulas, the one on the left is constructed using variables and and the one on the right is constructed using atomic propositions and :
The formula on the right is a single formula consisting of the atomic proposition and the formula connected by "". The formula on the left represents any formula consisting of two formulas connected with a "", where the second formula starts with a "". For example, the following are all instances of the formula on the left:
- : Let be and be .
- : Let be and be .
- : Let be and be
Note that we might encounter formulas that includes both variables and atomic propositions. For instance,
is a formula with one variable combined with the atomic proposition by the Boolean connnective "". The following are instances of the above formula:
- : Let be .
- : Let be .
- : Let be .
Terminology#
The following terminology will be used to refer to different parts of a formula:

Main Connective#
When reading a formula, the first thing you should do is identify the main connective. This will help identify the type of formula you are reading (i.e., is the formula a negation? a conjunction? a disjunction? a conditional?). The main connective of a formula is identified as follows:
- If the first symbol in the formula is "", then the first occurrence of "" is the main connective.
- Otherwise, the main connective is the first occurrence of the binary connective that is surrounded by the fewest number of parentheses.
For example, the main connective of is , and the main connective of is .
- Lecture
- Slides
Syntax Trees#
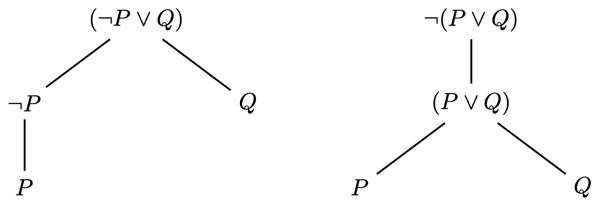
An important consequence of the definition for constructing formulas is that every formula has only one reading. That is, unlike in natural language, there is no (structural) ambiguity associated with a formula. Note that parentheses are needed to achieve a single reading for each formula. For instance, consider the following two formulas:
The reading of formula 1 is "either not or "; and the reading of formula 2 is "it is not the case that either or ". Without parentheses, the string
would be ambiguous between these two readings.
An important tool that helps visualize the readings of different formulas is a syntax tree (also called a parse tree). The main idea is that each formula can be turned into a diagram using the following rules:
Identify the main connective of the formula.
If the main connective is a unary connective, write the formula without the unary connective below the formula. If the main connective is a binary connective, then below the formula, write the left disjunct/left conjunct/antecedent to the left of the right disjunct/right conjunct/consequent. Draw a line connecting the formula to the formula(s) below it.
Repeat the above process until all formulas at the bottom of the diagram are atomic propositions.
For example, the syntax trees for formulas 1 and 2 are:
What is the syntax tree of ?
- Lecture
- Slides
What is the syntax tree of ?
- Lecture
- Slides
Other Connectives#
We used only four connectives when defining formulas. A natural question is: Why focus only on these four connectives? What about other binary connectives that are found in everyday reasoning and mathematical writing? We will return to these questions later in the text. A very useful connective that is not part of the definition of a formula is the biconditional. The biconditional is a binary connective, expressed with the symbol "", that means "...if, and only if,...". (Some texts use the "" symbol.) We can add this connective to the definition of a formula by adding the following clause to item 3 of the rules to construct formulas:
- If and are formulas, then is a formula.
However, for simplicity, it is more convenient to treat the biconditional as shorthand for a longer formula. We will say that "" is short for "". For example, the formula
is short for the formula
Simplifying Notation#
The use of parentheses in formulas ensures that every formula can be read in one way. The downside is that having too many parentheses in a formula can make the formula difficult to read. In order to simplify the notation, we will follow some conventions to allow some parentheses to be dropped from a formula. You are already familiar with this from algebra: is evaluated as rather than . We will adopt the following conventions to simplify the reading of formulas. (Other conventions are used in some logic texts, but we will only need the following three.)
- The outermost parentheses can be removed. For example, can be replaced with .
- Group conjunctions and disjunctions before conditionals (including the biconditional). For example,
- is the same as .
- is the same as .
- is the same as .
- Group conjunctions and disjunctions to the left before the ones on the right. For example,
- is the same as .
- is the same as .
- is the same as .
Practice Questions#
A. Identify the main connective of the following formulas.
B. For each of the following formulas, identify the left and right disjuncts.
C. For each of the following formulas, identify the left conjunct and the right conjunct.
D. For each of the following formulas, identify the antecedent and consequent.
E. Using the conventions defined in the section Simplifying Notation, add parentheses to rewrite the following formulas in official notation:
F. For each of the following questions, select the formula with variables such that the given formula is an instance of that formula.
G. Find the syntax trees for each of the following formulas: